What if we could rank order causal effects without having to estimate them? A creative question, but would it work?
Why would we want to rank rather than estimate at the first place? First, estimating causal effects is difficult and expensive. Also, in a case like the following, we may not need to estimate the effect: The decision to intervene has already been made (say, there will be a promotion). We want to maximize the return on the promotion.
A missing piece, as I also discussed with one of the authors is the estimation of the financial impact, which usually precedes the decision to intervene (and how). Let’s skip this part for now and assume that an intervention (a specific promotion) has already been decided. So the conditional question we are answering is: Which of the customers should we target given the promotion? Can we decide this without estimating the causal effect for each customer?
The paper explores two cases where causal effect ordering may be a viable solution:
- Intervention data is not available. In other words, we only have predictions of the treatment effect, not a direct estimate as we would have in an experiment. Let’s say we only have predicted propensity scores for conversion.
- Data on the actual outcome are not available, and we have to rely on a surrogate. Let’s say we can observe a customer’s short-term revenue, but that’s only a surrogate for the actual outcome we’re interested in: customer lifetime value.
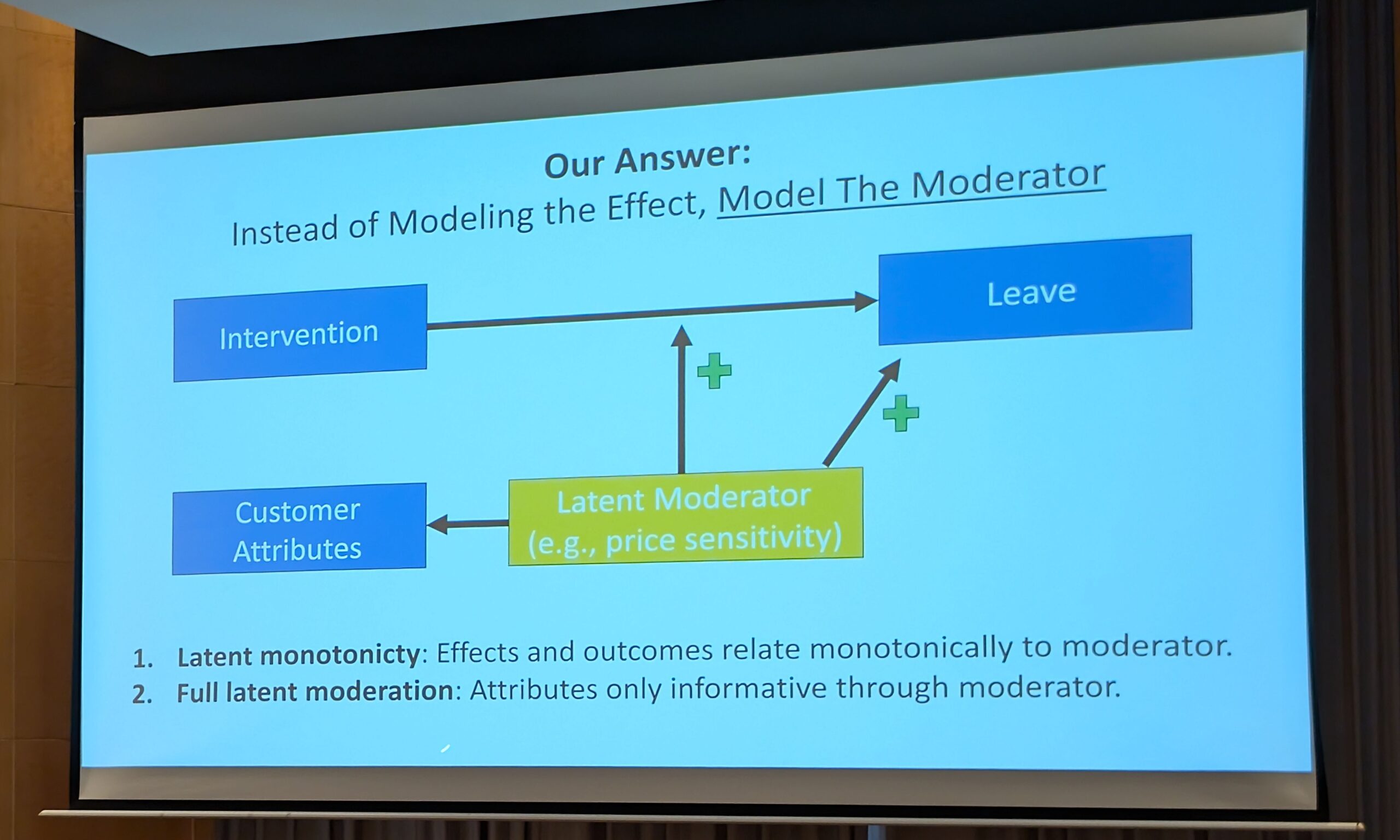
The authors use discrete choice modeling to show that in such cases where causal effect estimation is not feasible, causal effect ordering is possible if there exists a latent variable that satisfies the following two conditions:
- Latent monotonicity: The latent variable is monotonically (positively or negatively) related to both the treatment effect and the outcome.
- Full moderation: All (customer) features are informative only through the moderator.*
That is, following the example in the opening slide, customer features (demographics, historical and behavioral purchase patterns…) are only relevant to the effect of the promotion and the customer’s decision to leave the company through, let’s say, the customer’s price sensitivity (a perfect mediation).
Even with such strong assumptions, this looks like a useful and promising method. I came across this paper while attending a conference in December and finally found the time to take a look. Of course, there is more to the story. For example, what happens when you have multiple latent variables? If those latent variables are positively correlated, it shouldn’t be a problem, but what if they’re not? Also, the potentially different relationship between the latent variable and the outcome versus its surrogate is a concern. The authors address these boundary conditions and provide two decision trees in the paper that show when it is a good time to use causal effect ordering. Check it out here.
* The latent variable is actually a moderator of the relationship between the treatment and the outcome. The authors show how it can also be defined as a mediator between the features and the outcome (and its surrogate) when the treatment is removed from the DAG. See Figure 10 in the paper.